泊松分布是概率论中一种重要的离散分布，其描述的是单位时间内随机事件发生的次数。在比特币领域，泊松公式通常用于分析比特币区块的产生速度，帮助预测比特币网络的运行稳定性和未来发展趋势。

泊松公式的基本形式

泊松公式的基本形式如下：

\[ P(k; \lambda) = \frac{\lambda^k e^{\lambda}}{k!} \]

其中：

• \( P(k; \lambda) \) 表示在单位时间内随机事件发生 k 次的概率；
• \( \lambda \) 表示单位时间内事件发生的平均次数；

• \( e \) 是自然对数的底，约等于2.71828；
• \( k! \) 表示 k 的阶乘。

比特币中泊松公式的应用

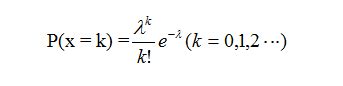
在比特币网络中，每个区块的产生速度理论上是遵循泊松分布的。比特币网络设定的区块产生的平均时间为约10分钟，因此 \( \lambda = \frac{1}{10} = 0.1 \)。

以比特币区块产生为例，假设我们想要计算在10分钟内产生 2 个区块的概率：

\[ P(2; 0.1) = \frac{0.1^2 e^{0.1}}{2!} \]

\[ P(2; 0.1) = \frac{0.01 \times 0.9048}{2} \]

\[ P(2; 0.1) ≈ 0.0045 \]

换句话说，产生 2 个区块的概率约为 0.45%。通过泊松公式的计算，我们可以进一步分析比特币网络在不同时间段内区块产生的稳定性，以及在网络拥堵或空闲情况下的表现。

泊松公式在比特币挖矿中的意义

对于比特币矿工而言，了解泊松分布在比特币挖矿中的应用意义十分重要。通过泊松公式的分析，矿工可以更好地掌握区块产生的规律，优化挖矿策略，提高挖矿效率，从而获取更多的比特币奖励。

矿工还可以利用泊松分布的特性，结合网络拓扑结构和计算能力，选择合适的挖矿节点，提高自己在比特币网络中的竞争力。

结语

泊松公式在比特币领域的应用有助于我们更深入地理解比特币网络的运行机制，帮助矿工和研究人员更好地分析网络数据和预测发展趋势。通过学习和应用泊松公式，我们可以更好地参与比特币生态，推动区块链技术的进步和发展。